Push Your Luck: Die Zukunft vorherwürfeln

Math is hard, let’s use python instead
~ Ich, bevor ich fünf Tage an einem Jupyter Notebook sitze
Push Your Luck: Das Testfeld
Für eine anschauliche Vorlesung über KI-Planung braucht es ein geeignetes Beispiel - so wart “Push Your Luck” geboren: simpel genug es schnell zu Verstehen, komplex genug für interessante KI-Strategien.
Die Spielregeln
Push Your Luck ist ein Würfelspiel für 2+ Spielende mit einem einfachen Prinzip: Sammle Punkte durch Würfeln, aber bei einer 1 verlierst du alles aus der aktuellen Runde.
Ziel: Als Erster 50 Punkte erreichen
Spielablauf:
- Würfeln: Wirf den W6
- Auswertung:
- Bei 1: Bust! Rundenpunkte verloren, Zug beendet
- Bei 2-6: Augenzahl zur Rundensumme addieren
- Entscheidung:
- Weiterwürfeln: Zurück zu Schritt 1 (Risiko: alles verlieren)
- Punkte sichern: Rundensumme zum Gesamtscore addieren, Zug beendet
Beispiel: Du würfelst 4, dann 6, dann 3 → Rundensumme: 13. Jetzt entscheidest du: Noch einen Wurf riskieren oder die 13 Punkte sichern?
Das Dilemma: Mehr Punkte bedeuten höheres Bust-Risiko. Diese Balance zwischen Gier und Vorsicht macht Push Your Luck zum
Die zentrale Herausforderung: Risiko vs. Belohnung optimal balancieren - ein ideales Testfeld für KI-Strategien.
Teil 1: Die Mathematischen Grundlagen
Bevor wir uns in die Welt der künstlichen Intelligenz stürzen, müssen wir erst einmal verstehen, womit wir es überhaupt zu tun haben. Push Your Luck mag auf den ersten Blick wie ein simples Glücksspiel aussehen, aber dahinter verbirgt sich eine faszinierende mathematische Struktur, die uns dabei hilft, optimale Strategien zu entwickeln.
Wahrscheinlichkeitstheorie – Wenn Mathematik zur Realität wird
Die fundamentale Frage, die man sich bei jedem Wurf stellt: Wie wahrscheinlich ist es eigentlich, dass ich als Nächstes eine 1 würfle und alles verliere?
Die Antwort ist einfach: Bei einem fairen sechsseitigen Würfel beträgt die Wahrscheinlichkeit für einen Bust genau , also etwa 16,7%. Umgekehrt bedeutet das: Die Wahrscheinlichkeit für einen sicheren Wurf liegt bei , also 83,3%.
Soweit, so simpel. Aber hier wird es interessant: Was passiert, wenn wir mehrfach würfeln? Dabei untersätzt man massiv, wie schnell das Risiko ansteigt. Das menschliche Gehirn ist notorisch schlecht darin, exponentielle Risiken richtig einzuschätzen.
Die Mathematik ist gnadenlos: Bei mehreren Würfen steigt das Bust-Risiko exponentiell an. Die Formel dafür lautet:
Diese Formel folgt einem einfachen Prinzip: Die Wahrscheinlichkeit, mindestens einmal eine 1 zu würfeln, ist das Gegenteil der Wahrscheinlichkeit, niemals eine 1 zu würfeln. Und die Wahrscheinlichkeit, niemals eine 1 zu würfeln, sinkt mit jedem zusätzlichen Wurf.
def calculate_bust_probability(rolls_remaining: int) -> float:
"""Berechnet Bust-Wahrscheinlichkeit für n verbleibende Würfe"""
if rolls_remaining <= 0:
return 0.0
no_bust_prob = 5.0 / 6.0
no_bust_all_rolls = no_bust_prob ** rolls_remaining
return 1.0 - no_bust_all_rollsDie Zahlen sind erschreckend: Bereits nach 4 Würfen überschreitet die Bust-Wahrscheinlichkeit die 50%-Marke. Nach 10 Würfen liegt sie bei beeindruckenden 83,8%, und wer wagemutig genug ist, 20 Mal zu würfeln, hat eine 97,4%ige Chance, mit leeren Händen dazustehen.
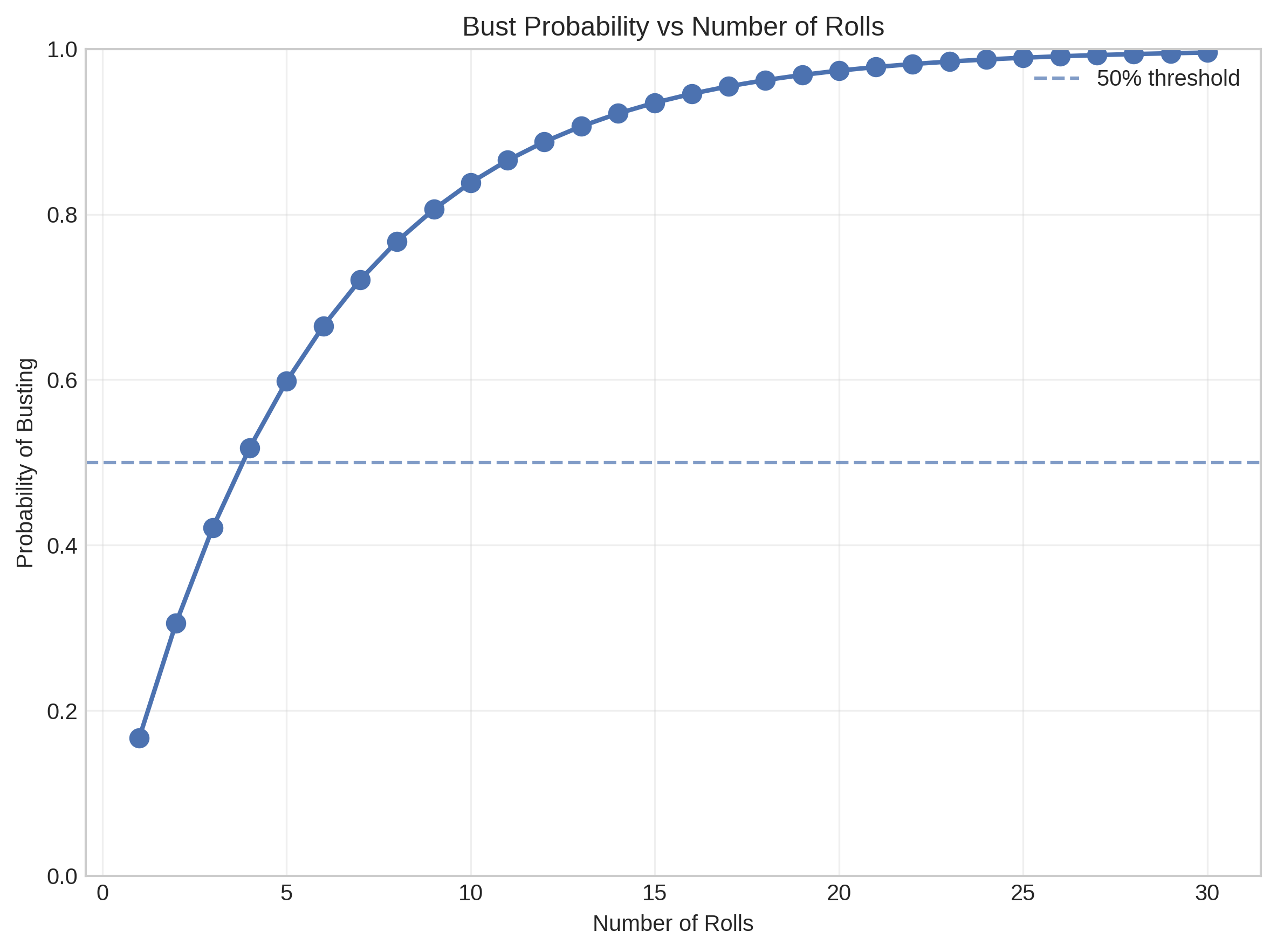
Dieser Graph zeigt eindrucksvoll, wie rasant das Bust-Risiko ansteigt. Diese kritischen Schwellenwerte zeigen uns bereits jetzt: Jede vernünftige Strategie muss irgendwann sagen: “Schluss jetzt, ich sichere meine Punkte.”
Expected Value Theory – Rationale Entscheidungen den Zufall betrachtend
Aber wann genau sollte man aufhören? Hier kommt der Expected Value (EV - Erwartungswert auf Deutsch) ins Spiel – ein Konzept, das nicht nur in der Spieltheorie, sondern auch in der Finanzwelt und bei strategischen Entscheidungen eine zentrale Rolle spielt.
Der Expected Value ist im Grunde eine simple Frage: “Was ist der durchschnittliche Wert meiner Entscheidung, wenn ich sie unendlich oft wiederholen würde?” Bei Push Your Luck haben wir an jedem Entscheidungspunkt zwei Optionen:
- Bank: Sichere Punkte = aktuelle Rundensumme (garantiert, kein Risiko)
- Continue: Erwartungswert bei Fortsetzung (unsicher, aber potenziell höher)
Die mathematisch optimale Entscheidung ist immer die mit dem höheren Expected Value.
Ein-Wurf-Analyse – Der einfachste Fall
Beginnen wir mit dem simpelsten Szenario: Was passiert, wenn wir genau einen weiteren Wurf machen und dann definitiv banken?
Angenommen, wir haben bereits Punkte in unserer Rundensumme. Bei einem weiteren Wurf können folgende Dinge passieren:
- Mit Wahrscheinlichkeit würfeln wir eine 1 und bekommen 0 Punkte
- Mit Wahrscheinlichkeit würfeln wir eine 2 und bekommen Punkte
- … und so weiter bis zur 6
Die mathematische Formel für diesen Ein-Wurf-Expected-Value lautet:
Diese Formel tells us something fascinating: Der Expected Value eines weiteren Wurfs steigt linear mit unserer aktuellen Rundensumme. Das macht intuitiv Sinn – je mehr wir bereits haben, desto wertvoller wird ein erfolgreicher Wurf.
Rekursive Optimierung – Das große Ganze
Aber natürlich ist die Realität komplexer. Wir müssen nicht nach genau einem Wurf aufhören – wir können nach jedem Wurf neu entscheiden. Das führt uns zur rekursiven Optimierung, einem Kernkonzept der Spieltheorie.
Die optimale Strategie ergibt sich aus der folgenden Gleichung:
Diese Gleichung besagt: Der optimale Expected Value bei Rundensumme ist das Maximum aus zwei Optionen:
- Sofort banken und Punkte sicher bekommen
- Weiterwürfeln und den Expected Value aller möglichen Folgezustände bekommen
Durch Rückwärtsinduktion – ein Verfahren, bei dem wir vom Ende her denken – lässt sich diese Gleichung lösen. Das Ergebnis ist verblüffend: Der optimale Schwellenwert liegt bei etwa 20 Punkten.
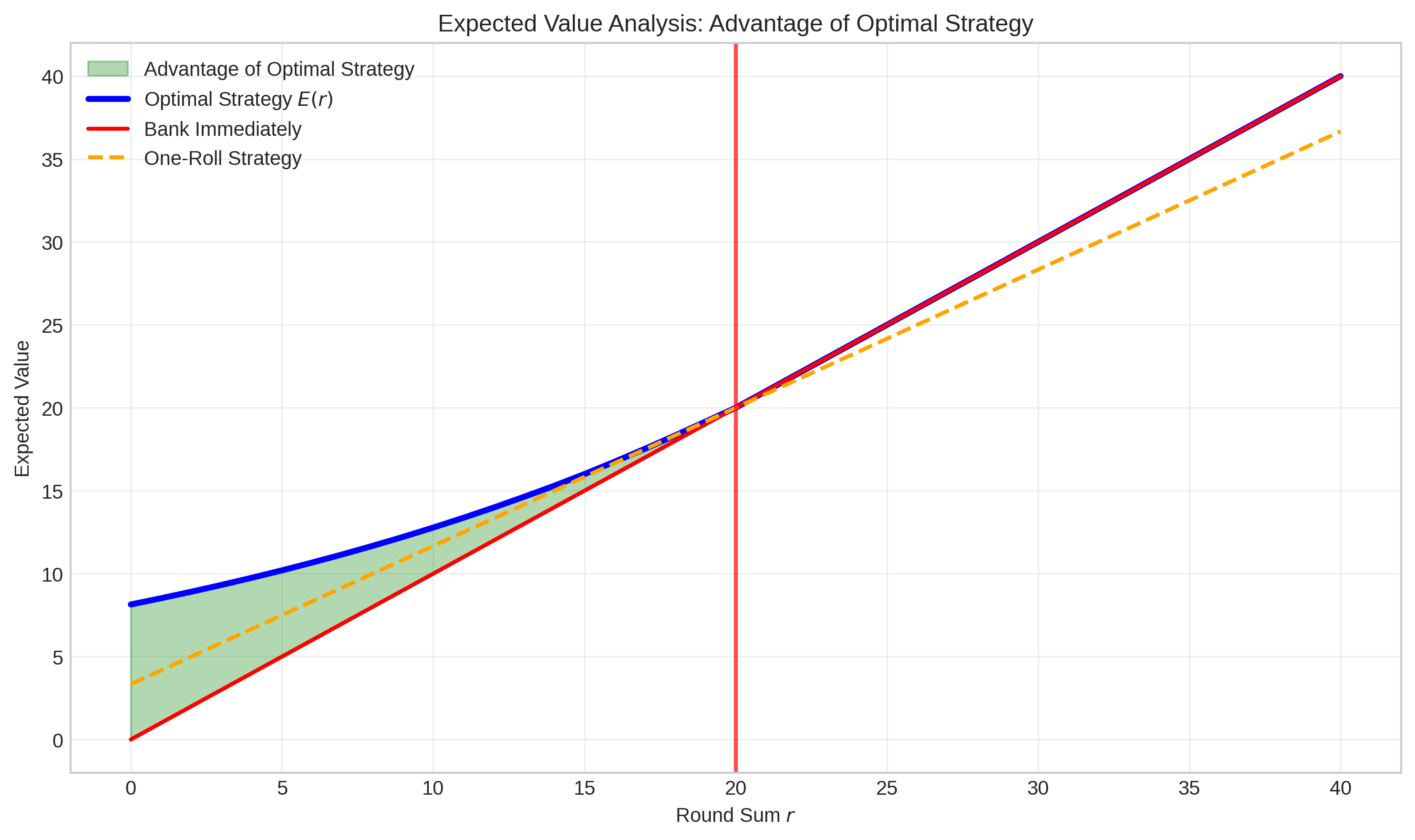
Die grüne Fläche in diesem Diagramm zeigt den mathematischen Vorteil der optimalen Strategie gegenüber dem sofortigen Banking. Der kritische Punkt liegt bei 20 Punkten (rote Linie) – hier kreuzen sich die Strategien und ab diesem Moment wird Banking zur besseren Option als Weiterwürfeln, da weiterwürfeln keinen zusätzlichen Vorteil bietet.
# Berechnung des optimalen Schwellenwerts
max_r = 40
E = np.zeros(max_r + 7)
for r in range(max_r, -1, -1):
expected_roll = E[r+2:r+7].sum() / 6.0
E[r] = max(r, expected_roll)
# Optimaler Threshold: wo E[r] ≈ rDieser Code implementiert die Rückwärtsinduktion: Wir starten bei hohen Rundensummen (wo banking offensichtlich optimal ist) und arbeiten uns nach unten vor. Für jede Rundensumme berechnen wir den Expected Value des Weiterwürfelns und vergleichen ihn mit dem sicheren Banking-Wert.
Das Ergebnis zeigt uns: Mathematisch gesehen sollten wir immer weiterwürfeln, bis wir 20 Punkte erreicht haben. Darunter ist das Risiko den potenziellen Gewinn wert, darüber überwiegt die Gefahr.
Diese 20-Punkte-Regel wird zur Grundlage unserer ersten intelligenten KI werden – einer Artificial Intelligence, die rein auf mathematischer Optimierung basiert.
Teil 2: Erste KI-Implementierungen
Jetzt, da wir die mathematischen Grundlagen verstehen, können wir unsere ersten künstlichen Intelligenzen entwickeln. Aber bevor wir uns in die Tiefen von Machine Learning und neuronalen Netzen stürzen, beginnen wir mit etwas Einfacherem: regelbasierten Systemen.
Diese ersten KI-Ansätze mögen simpel erscheinen, aber sie lehren uns wichtige Lektionen über Strategieentwicklung, Risikomanagement und – wie wir noch sehen werden – die Grenzen simpler mathematischer Optimierung.
Random AI: Der Zufall als Baseline
class RandomAI:
def __init__(self, name: str, aggression: float = 0.5):
self.name = name
self.aggression = aggression
def make_decision(self, game_state: GameState) -> PlayerAction:
if game_state.current_round_sum == 0:
return PlayerAction.CONTINUE_ROLLING
if random.random() < self.aggression:
return PlayerAction.CONTINUE_ROLLING
else:
return PlayerAction.BANK_POINTSUnsere erste KI ist zugleich die einfachste und eine der wichtigsten: eine vollkommen zufällige Künstliche Intelligenz. Das mag kontraproduktiv klingen – warum sollten wir bewusst eine schlechte KI entwickeln? – aber in der KI-Forschung ist ein zufälliger Baseline unverzichtbar.
Die Random AI funktioniert nach einem simplen Prinzip: Sie trifft ihre Entscheidungen basierend auf einem “Aggressionslevel”. Ist dieses auf 0.5 gesetzt, würfelt sie bei jedem Entscheidungspunkt eine Münze – Kopf bedeutet weiterwürfeln, Zahl bedeutet banken. Bei einem Aggressionslevel von 0.8 würfelt sie in 80% der Fälle weiter, bei 0.2 nur in 20%.
Diese Random AI dient uns als Referenzpunkt. Jede ernsthafte KI-Strategie muss besser sein als purer Zufall – sonst können wir gleich würfeln, anstatt komplexe Algorithmen zu entwickeln. Außerdem zeigt uns die Random AI etwas Faszinierendes über Push Your Luck: Selbst mit völlig zufälligen Entscheidungen gewinnt sie gelegentlich Spiele. Das Glück spielt also immer eine Rolle, egal wie smart unsere Strategie ist.
Conservative AI: Sicherheit First
class ConservativeAI:
def __init__(self, name: str, bank_threshold: int = 8):
self.name = name
self.bank_threshold = bank_threshold
def make_decision(self, game_state: GameState) -> PlayerAction:
if game_state.current_round_sum >= self.bank_threshold:
return PlayerAction.BANK_POINTS
else:
return PlayerAction.CONTINUE_ROLLINGAm anderen Ende des Risikospektrums steht unsere Conservative AI – eine KI, die das Motto “Lieber einen Spatz in der Hand als eine Taube auf dem Dach” verinnerlicht hat. Ihre Strategie ist denkbar einfach: Sobald sie eine bestimmte Punktzahl in ihrer Rundensumme erreicht hat (typischerweise 8 Punkte), bankt sie sofort.
Diese Herangehensweise spiegelt wider, wie viele Menschen in unsicheren Situationen reagieren: Sie bevorzugen die Sicherheit gegenüber dem Risiko. Die Conservative AI ist der Typ Mensch, der beim Investieren nur auf Festgeld setzt oder der beim Pokern foldet, sobald der Einsatz steigt.
Der Vorteil dieser Strategie liegt auf der Hand: Sie produziert sehr konsistente Ergebnisse. Die Conservative AI wird selten katastrophal verlieren, weil sie nie große Risiken eingeht. Ihre Varianz ist niedrig – ein statistischer Begriff dafür, dass ihre Ergebnisse vorhersagbar sind.
Aber diese Sicherheit hat ihren Preis: Die Conservative AI wird auch selten große Sprünge machen. In Situationen, wo Aggressivität gefragt ist – etwa wenn sie deutlich zurückliegt –, fehlt ihr die Flexibilität, ihre Strategie anzupassen.
Aggressive AI: High Risk, High Reward
class AggressiveAI:
def make_decision(self, game_state: GameState) -> PlayerAction:
my_score = game_state.player_scores[game_state.current_player]
max_opponent_score = max(other_scores) if other_scores else 0
threshold = self.bank_threshold
if my_score < max_opponent_score:
threshold += 5 # Aggressiver wenn hinten
if game_state.current_round_sum >= threshold:
return PlayerAction.BANK_POINTS
else:
return PlayerAction.CONTINUE_ROLLINGDie Aggressive AI ist das Gegenteil der Conservative AI: Sie lebt nach dem Motto “Wer nicht wagt, der nicht gewinnt”. Mit einem hohen Banking-Schwellenwert von 18-20 Punkten geht sie bewusst größere Risiken ein, um höhere Belohnungen zu erzielen.
Aber hier zeigt sich bereits etwas Cleveres: Die Aggressive AI ist nicht blind aggressiv. Sie berücksichtigt ihre Position im Spiel. Liegt sie zurück, wird sie noch riskanter und erhöht ihren Schwellenwert um weitere 5 Punkte. Führt sie hingegen, kann sie es sich leisten, etwas vorsichtiger zu sein.
Diese Kontextbewusstsein ist ein wichtiger Schritt in Richtung intelligenter Strategien. Die Aggressive AI versteht, dass Push Your Luck nicht im Vakuum stattfindet – es ist ein Rennen gegen andere Teilnehmende. Diese Erkenntnis wird später noch entscheidend werden.
Probabilistic AI: Die mathematische Optimierung
class ProbabilisticAI:
def __init__(self, name: str, optimal_threshold: int = 20):
self.name = name
self.optimal_threshold = optimal_threshold
def make_decision(self, game_state: GameState) -> PlayerAction:
current_sum = game_state.current_round_sum
if current_sum == 0:
return PlayerAction.CONTINUE_ROLLING
ev_continue = (5 * current_sum + self.optimal_threshold) / 6
ev_bank = float(current_sum)
if ev_continue > ev_bank:
return PlayerAction.CONTINUE_ROLLING
else:
return PlayerAction.BANK_POINTSUnd dann haben wir unsere vermeintliche Kronjuwel: die Probabilistic AI, auch “Smart Sam” genannt. Diese KI implementiert die mathematische Optimierung, die wir im ersten Teil entwickelt haben. Sie berechnet für jede Situation den Expected Value des Weiterwürfelns und vergleicht ihn mit dem sicheren Banking-Wert.
Smart Sam ist, mathematisch gesehen, die optimale Lösung für Push Your Luck. Sie nutzt die 20-Punkte-Regel, die wir durch Rückwärtsinduktion berechnet haben. Jede ihrer Entscheidungen maximiert den erwarteten Gewinn. Sie ist die Verkörperung rationaler Entscheidungsfindung.
Eigentlich sollte Smart Sam alle anderen KIs dominieren. Schließlich basiert sie auf mathematischer Perfektion, während die anderen nur auf einfachen Heuristiken beruhen.
Das große Turnier: Wenn Theorie auf Realität trifft
Zeit für den ultimativen Test: Wir lassen alle unsere KIs in einem großen Turnier gegeneinander antreten. 10.000 Spiele, vier verschiedene Strategien, ein klares Ziel: Herausfinden, welcher Ansatz in der Praxis wirklich funktioniert.
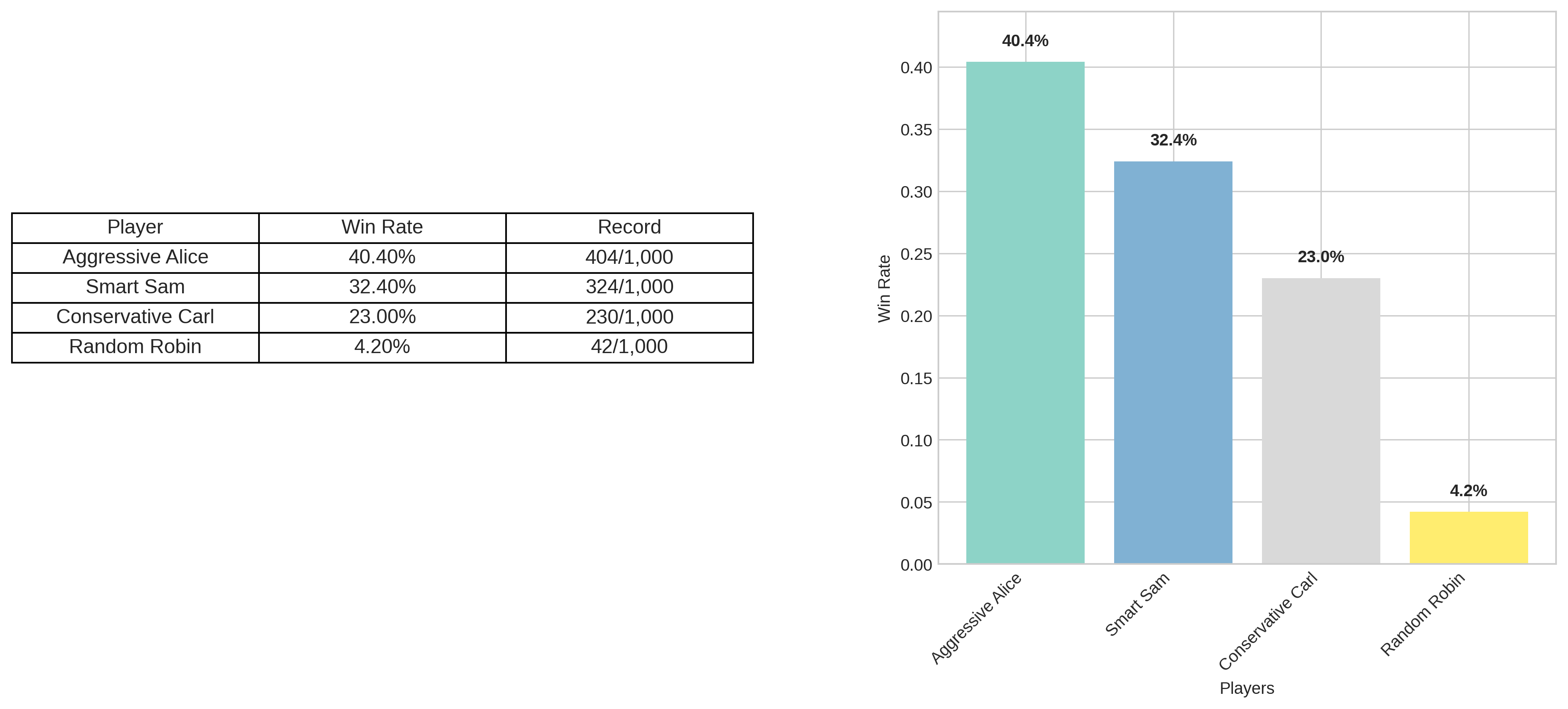
Das Ergebnis ist verblüffend – und ernüchternd zugleich. Aggressive Alice gewinnt mit 40,4% der Spiele, während unsere mathematisch “perfekte” Smart Sam nur auf 32,4% kommt. Selbst die simple Conservative Carl schlägt sich mit 23% respektabel, während Random Robin erwartungsgemäß mit 4,2% das Schlusslicht bildet.
Aber moment – das kann doch nicht sein! Smart Sam nutzt die mathematisch optimale Strategie. Sie maximiert den Expected Value in jeder einzelnen Situation. Wie kann eine simple Aggressive AI sie übertreffen?
Das Problem mit den bisherigen Berechnungen
Hier offenbart sich ein fundamentales Problem unserer bisherigen Herangehensweise: Smart Sam optimiert für das falsche Ziel. Sie maximiert ihre erwarteten Punkte pro Runde, aber Push Your Luck ist kein Punktesammelspiel – es ist ein Rennen.
Die mathematische Optimierung, die wir entwickelt haben, behandelt jede Entscheidung isoliert. Sie fragt: “Soll ich in dieser spezifischen Situation weiterwürfeln oder banken?” Die Antwort basiert ausschließlich auf der aktuellen Rundensumme und den Wahrscheinlichkeiten.
Was Smart Sam völlig ignoriert:
- Wo steht sie im Vergleich zu den Gegnenden?
- Wie aggressiv spielen die anderen?
- Ist sie bereits nah am Ziel oder muss sie aufholen?
- Befinden wir uns in der Anfangs-, Mittel- oder Endphase des Spiels?
Aggressive Alice hingegen macht intuitiv das Richtige: Sie passt ihre Strategie an den Kontext an. Liegt sie zurück, wird sie aggressiver. Das ist nicht mathematisch optimal für einzelne Züge, aber es ist strategisch intelligent für das Gesamtspiel.
Die Erkenntnis: Kontext schlägt Optimierung
Dieses Turnierergebnis lehrt uns eine wichtige Lektion über KI und Entscheidungsfindung: Lokale Optimierung führt nicht automatisch zu globaler Performance. Die beste Einzelentscheidung ist nicht immer die beste Gesamtstrategie.
Smart Sam spielt, als wäre sie allein auf der Welt. Sie optimiert jeden Zug perfekt, aber sie vergisst dabei, dass sie sich in einem Wettkampf befindet. Es ist, als würde man den perfekten Marathon-Laufstil entwickeln, aber dabei vergessen, dass da noch andere Läufende sind, die man überholen muss.
Diese Erkenntnis bringt uns zur nächsten Evolutionsstufe der KI-Entwicklung: Wir müssen vom Expected Value zum tatsächlichen Spielziel übergehen. Statt “Wie maximiere ich meine Punkte?” müssen wir fragen: “Wie maximiere ich meine Gewinnwahrscheinlichkeit?”
Und diese Frage führt uns direkt in die Welt des Dynamic Programming – wo Kontext und mathematische Optimierung endlich zusammenfinden.
Teil 3: Dynamic Programming - Der Spielstand zählt
Win Probability statt Expected Points – Ein Paradigmenwechsel
Unsere bisherige Herangehensweise hatte einen fundamentalen Denkfehler: Wir haben versucht, die erwarteten Punkte zu maximieren, obwohl das Ziel von Push Your Luck nicht darin besteht, möglichst viele Punkte zu sammeln. Das Ziel ist es zu gewinnen – und das ist ein völlig anderes Problem.
Dieser Unterschied mag subtil erscheinen, ist aber entscheidend. Stelle dir vor, du führst mit 47 zu 20 Punkten. In dieser Situation wäre es völlig irrational, noch 15 weitere Punkte zu riskieren, nur weil der Expected Value das nahelegt. Drei sichere Punkte reichen zum Sieg – alles andere ist unnötiges Risiko.
Das neue Ziel lautet daher: Gewinnwahrscheinlichkeit maximieren statt Expected Points maximieren. Diese Änderung der Zielfunktion erfordert eine völlig neue mathematische Herangehensweise: Dynamic Programming.
Dynamic Programming – Die Kunst der optimalen Entscheidungssequenzen
Dynamic Programming (DP) ist eine der elegantesten Methoden der Informatik und Mathematik. Die Grundidee ist einfach: Komplexe Probleme lassen sich lösen, indem man sie in kleinere, überschaubare Teilprobleme zerlegt und diese systematisch von hinten nach vorne löst.
Stelle dir vor, du müsstest den kürzesten Weg von Berlin nach München finden. Statt alle möglichen Routen zu durchsuchen, könntest du das Problem umdrehen: “Wenn ich bereits in Nürnberg bin, wie komme ich am schnellsten nach München?” Dann: “Wenn ich in Frankfurt bin, wie komme ich am schnellsten nach Nürnberg?” Und so weiter, bis du in Berlin angekommen bist.
Bei Push Your Luck funktioniert das genauso: Wir beginnen mit Situationen, in denen die optimale Entscheidung offensichtlich ist (z.B. “Ich habe 49 Punkte und 2 in der Rundensumme – natürlich banke ich”), und arbeiten uns systematisch zu komplexeren Situationen vor.
Der Zustandsraum – Vollständige Beschreibung der Spielsituation
Für Dynamic Programming benötigen wir eine präzise Definition dessen, was einen “Zustand” im Spiel ausmacht. Welche Informationen sind notwendig, um eine optimale Entscheidung zu treffen?
Bei Push Your Luck besteht ein vollständiger Spielzustand aus drei Komponenten:
- : Mein aktueller Gesamtpunktestand
- : Der Punktestand meiner stärksten Konkurrenz
- : Meine aktuelle Rundensumme (die Punkte, die auf dem Spiel stehen)
Diese drei Zahlen enthalten alle Informationen, die für eine optimale Entscheidung relevant sind. Mehr brauchen wir nicht – weniger würde wichtige Informationen auslassen.
Ein Beispiel: Der Zustand bedeutet: Ich habe 35 Punkte, meine stärkste Konkurrenz hat 40 Punkte, und ich habe derzeit 12 Punkte in meiner Rundensumme. Diese Situation erfordert eine andere Strategie als – obwohl die Rundensumme identisch ist.
Die Win-Probability Bellman-Gleichung – Mathematische Präzision
Das Herzstück unseres Dynamic Programming-Ansatzes ist die Bellman-Gleichung. Sie beschreibt, wie sich die Gewinnwahrscheinlichkeit eines Zustands aus den Gewinnwahrscheinlichkeiten der Folgezustände ergibt.
Für jeden Zustand haben wir zwei Optionen:
Option 1: Banking
Diese Formel beschreibt, was passiert, wenn wir unsere Rundenpunkte sichern. Unsere Rundensumme wird zu unserem Gesamtstand addiert, die Rundensumme wird auf 0 zurückgesetzt, und der Gegner ist am Zug. bezeichnet dabei die Gewinnwahrscheinlichkeit nach dem Gegnerzug.
Option 2: Weiterwürfeln
Beim Weiterwürfeln gibt es zwei Szenarien: Mit Wahrscheinlichkeit busten wir (würfeln eine 1), verlieren alle Rundenpunkte und der Gegner ist dran. Mit Wahrscheinlichkeit würfeln wir eine 2-6, addieren den Wert zu unserer Rundensumme und stehen vor der gleichen Entscheidung – nur mit höherer Rundensumme und damit höherem Risiko.
Die optimale Entscheidung
Diese Gleichung ist die mathematische Formalisierung der optimalen Strategie: Wähle immer die Option mit der höheren Gewinnwahrscheinlichkeit. Es ist die Essenz rationaler Entscheidungsfindung in mathematischer Form.
Opponent Turn Modeling mit P’
Die Funktion modelliert, was nach unserem Zug passiert – den Gegnerzug:
Dabei ist die Anzahl Punkte, die der Gegner in seinem Zug gewinnt (0 bei Bust, 2+ bei erfolgreichem Banking). ist die Wahrscheinlichkeit, dass der Gegner genau Punkte gewinnt. Diese Wahrscheinlichkeiten ermitteln wir durch Monte Carlo Simulation.
Monte Carlo Opponent Modeling – Simulation statt Analyse
Nun haben wir ein Problem: Um zu berechnen – die Gewinnwahrscheinlichkeit nach dem Gegnerzug –, müssen wir wissen, wie sich das Gegenüber verhält. Aber verschiedene KI-Typen haben völlig unterschiedliche Strategien. Wie modellieren wir das?
Hier kommt Monte Carlo Simulation ins Spiel – eine Technik, die ihren Namen den berühmten Casinos von Monte Carlo verdankt. Die Grundidee: Statt komplexe mathematische Formeln zu entwickeln, simulieren wir einfach tausende von Gegnerzügen und schauen, was dabei herauskommt.
Monte Carlo: Lernen durch Wiederholung
Monte Carlo-Methoden basieren auf dem Gesetz der großen Zahlen: Wenn wir einen zufälligen Prozess oft genug wiederholen, nähern sich die beobachteten Häufigkeiten den wahren Wahrscheinlichkeiten an. Das ist dasselbe Prinzip, nach dem Casinos funktionieren – einzelne Spielerinnen können gewinnen, aber bei tausenden von Spielen setzen sich die mathematischen Wahrscheinlichkeiten durch.
In unserem Fall simulieren wir für jeden Gegnertyp und jeden möglichen Startpunktestand tausende von Zügen. Eine Conservative AI mit 25 Punkten verhält sich völlig anders als eine Aggressive AI mit 45 Punkten – und durch Simulation können wir diese Unterschiede präzise erfassen.
def simulate_opponent_turn(opponent: Player, starting_score: int) -> int:
"""Simuliert einen Gegnerzug, gibt gewonnene Punkte zurück"""
game_state = GameState(
player_scores=(starting_score, 0),
current_player=0,
current_round_sum=0,
game_over=False,
winner=None
)
points_gained = 0
while not game_state.game_over and game_state.current_player == 0:
action = opponent.make_decision(game_state)
if action == PlayerAction.BANK_POINTS:
points_gained = game_state.current_round_sum
break
elif action == PlayerAction.CONTINUE_ROLLING:
roll_result = roll_dice()
if roll_result.is_bust:
points_gained = 0 # Bust
break
else:
game_state = game_state._replace(
current_round_sum=game_state.current_round_sum + roll_result.value
)
return points_gainedDer Simulationsprozess
Für jeden Gegnertyp erstellen wir eine Wahrscheinlichkeitsverteilung: “Wenn diese KI bei Punktestand X am Zug ist, mit welcher Wahrscheinlichkeit gewinnt sie Y zusätzliche Punkte?”
Beispielsweise könnte eine Conservative AI bei 20 Punkten folgende Verteilung haben:
- 30% Wahrscheinlichkeit für 0 Punkte (Bust)
- 25% Wahrscheinlichkeit für 8 Punkte (bankt bei ihrem Schwellenwert)
- 20% Wahrscheinlichkeit für 9 Punkte
- 15% Wahrscheinlichkeit für 10 Punkte
- … und so weiter
Diese Verteilungen entstehen durch tausende von Simulationen. Wir lassen die Conservative AI von jedem möglichen Startpunktestand aus spielen, beobachten das Ergebnis, und erstellen daraus eine statistische Verteilung.
Warum Monte Carlo statt analytische Lösung?
Monte Carlo ist universell anwendbar. Eine analytische Lösung müsste für jeden Gegnertyp individuell entwickelt werden. Für eine Simple Conservative AI wäre das noch machbar, aber für komplexere Strategien würde die Mathematik schnell unüberschaubar.
Monte Carlo hingegen funktioniert mit jeder beliebigen Gegnerstrategie. Selbst wenn wir später neuronale Netze oder andere Black-Box-Systeme als Gegner haben, können wir sie einfach simulieren, ohne ihre interne Logik verstehen zu müssen.
Die DP-Implementation – Von der Theorie zur Praxis
Mit den Monte Carlo-Verteilungen können wir nun das Dynamic Programming umsetzen. Der Prozess läuft in zwei Phasen ab:
Phase 1: Datensammlung Für jeden Gegnertyp simulieren wir tausende von Zügen bei verschiedenen Startpunkteständen. Das Ergebnis sind Wahrscheinlichkeitsverteilungen für die Punktgewinne.
Phase 2: Rückwärtsinduktion Wir berechnen die optimalen Strategien durch Rückwärtsinduktion. Die Kernberechnung für einen einzelnen Zustand sieht so aus:
def compute_state_value(my_score: int, opp_score: int, round_sum: int,
opponent_dist: dict, dp: dict) -> dict:
"""Berechnet optimale Gewinnwahrscheinlichkeit und Aktion für einen Zustand"""
# Terminale Zustände
if my_score >= 50 or my_score + round_sum >= 50:
return {'win_prob': 1.0, 'action': PlayerAction.BANK_POINTS}
if opp_score >= 50:
return {'win_prob': 0.0, 'action': PlayerAction.CONTINUE_ROLLING}
# Vergleiche P_bank vs P_continue
bank_value = compute_P_bank(my_score, opp_score, round_sum, opponent_dist, dp)
continue_value = compute_P_continue(my_score, opp_score, round_sum, opponent_dist, dp)
if bank_value >= continue_value:
return {'win_prob': bank_value, 'action': PlayerAction.BANK_POINTS}
else:
return {'win_prob': continue_value, 'action': PlayerAction.CONTINUE_ROLLING}Das Ergebnis der DP-Berechnung ist eine riesige Lookup-Tabelle. Für jeden möglichen Zustand speichern wir zwei Informationen:
- Die optimale Gewinnwahrscheinlichkeit von diesem Zustand aus
- Die optimale Aktion (bank oder continue)
Diese Tabelle ist unsere perfekte Strategie gegen den jeweiligen Gegnertyp. Zur Laufzeit müssen wir nur noch den aktuellen Zustand nachschlagen und die gespeicherte Aktion ausführen.
Monte Carlo DP AI – Die perfekte Spielerin
Mit all diesen Komponenten können wir nun unsere erste wirklich intelligente KI entwickeln:
class MonteCarloDP_AI:
"""AI mit Monte Carlo Gegnermodellierung und Dynamic Programming"""
def __init__(self, name: str):
self.name = name
self.dp_tables = {}
def setup(self, distributions: dict) -> None:
"""Berechnet optimale Strategien gegen alle Gegnertypen vor"""
for opponent_name in distributions.keys():
self.dp_tables[opponent_name] = solve_win_probability_dp(
distributions, opponent_name
)
def make_decision(self, game_state: GameState) -> PlayerAction:
"""Trifft Entscheidung mit Ensemble optimaler Strategien"""
my_score = game_state.player_scores[game_state.current_player]
opp_score = max(other_scores) if other_scores else 0
round_sum = game_state.current_round_sum
# Ensemble-Voting über Gegnermodelle
votes = {'bank': 0, 'continue': 0}
for opponent_name, dp_table in self.dp_tables.items():
key = (my_score, opp_score, round_sum)
if key in dp_table:
action = dp_table[key]['action']
if action == PlayerAction.BANK_POINTS:
votes['bank'] += 1
else:
votes['continue'] += 1
return PlayerAction.BANK_POINTS if votes['bank'] >= votes['continue'] else PlayerAction.CONTINUE_ROLLINGKomplexitätsanalyse – Grenzen der Perfektion
Dynamic Programming hat einen Haken: Die Anzahl der Zustände explodiert mit der Anzahl der Spielenden. Bei zwei Personen haben wir noch etwa 75.000 Zustände – das ist problemlos handhabbar. Bei vier Personen sind es bereits 187 Millionen Zustände, was 1,5 GB Speicher erfordert.
| Spielende | Komplexität | Zustände (50 Punkte Ziel) | Speicherbedarf |
|---|---|---|---|
| 2 | O(target² × max_round) | 75.000 | 600 KB |
| 3 | O(target³ × max_round) | 3.750.000 | 30 MB |
| 4 | O(target⁴ × max_round) | 187.500.000 | 1.5 GB |
Für Push Your Luck mit mehr als drei Spielenden wird Dynamic Programming unpraktikabel. Das ist ein fundamentales Problem vieler exakter Optimierungsverfahren: Sie liefern perfekte Ergebnisse, aber nur für kleine Probleminstanzen.
Die Lösung: Approximation
Für Mehrspielerspiele verwenden wir eine einfache Approximation: Wir betrachten nur den führenden Gegner. Das reduziert die Komplexität wieder auf das handhabbare Niveau von zwei Spielenden.
Diese Approximation ist nicht perfekt, aber sie ist gut genug für praktische Zwecke und macht Dynamic Programming auch für größere Spiele anwendbar.
Mit dieser Grundlage haben wir endlich unsere erste wirklich intelligente KI entwickelt: eine, die nicht nur mathematisch optimiert, sondern auch den Kontext des Spiels versteht. Diese Monte Carlo DP AI wird zur Benchmark für alle weiteren Entwicklungen – der Goldstandard, an dem sich andere Ansätze messen müssen.
Das Turnierergebnis – Dynamic Programming dominiert
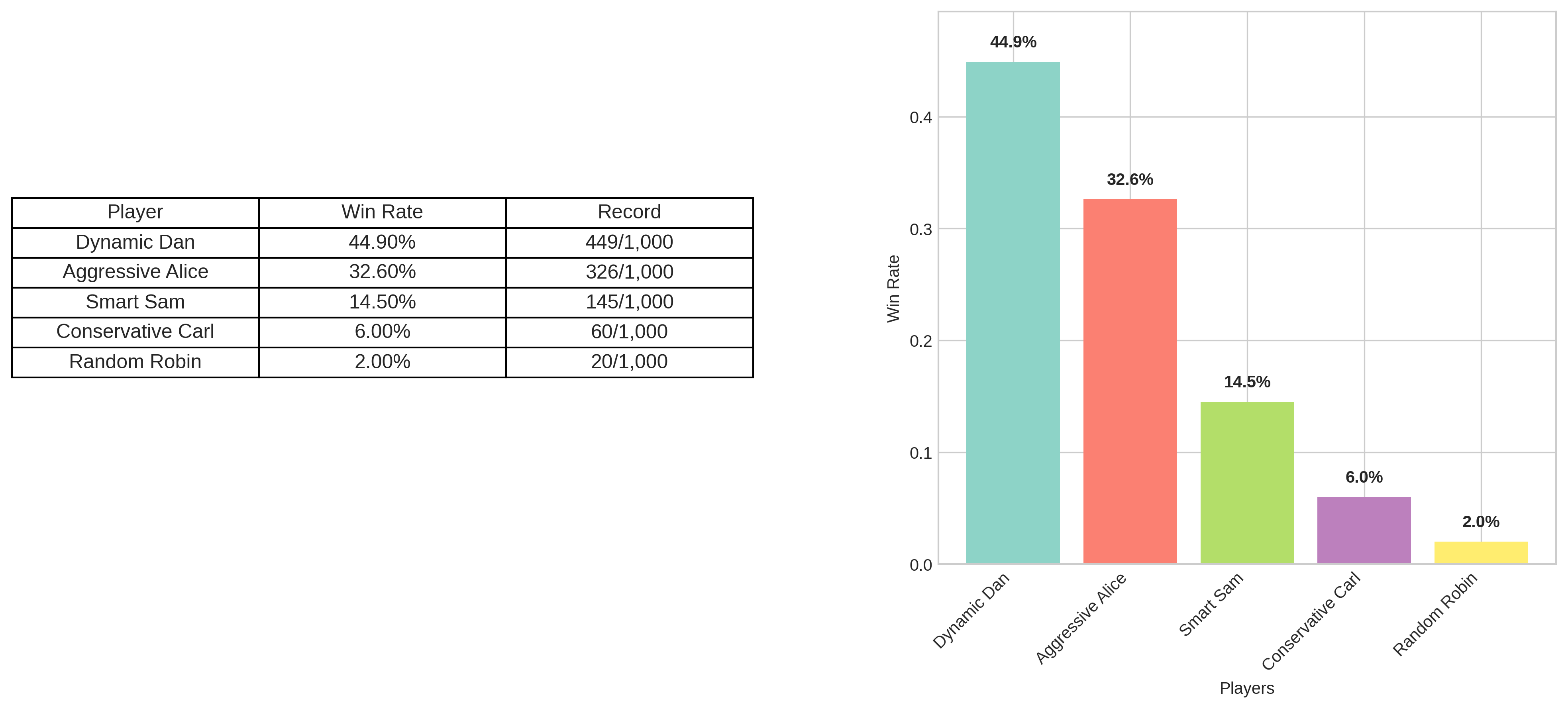
Der finale Test bestätigt unsere Theorie: Dynamic Dan gewinnt mit 44,9% der Spiele und dominiert damit alle anderen Ansätze. Besonders bemerkenswert ist der Kollaps von Smart Sam auf nur noch 14,5% – die kontextlose mathematische Optimierung ist gegen eine kontextbewusste Strategie chancenlos. Dynamic Programming beweist eindrucksvoll: Die beste lokale Entscheidung ist nicht immer die beste globale Strategie.
Teil 4: Neuronale Netze - Von Tabellen zu Funktionen
Die Grenzen der Perfektion
Unsere Dynamic Programming AI ist mathematisch perfekt – aber sie hat einen entscheidenden Nachteil: Sie ist unglaublich starr. Für jeden einzelnen Gegnertyp müssen wir eine komplette Lookup-Tabelle mit 75.000 Einträgen berechnen. Will man gegen einen neuen Gegner spielen? Stundenlange Neuberechnung. Ändert sich eine Spielregel minimal? Alles von vorne.
Das ist, als hätte man für jede denkbare Verkehrssituation eine perfekte Anweisung auswendig gelernt: “Bei Regen auf der A9 mit einem roten BMW vor dir bei 80 km/h: bremse um 2 km/h ab.” Funktioniert perfekt – aber nur, wenn man wirklich jede Situation vorhergesehen hat.
Besser: Lernen statt Auswendiglernen
Was wäre, wenn unsere KI stattdessen Muster erkennen könnte? Wenn sie verstehen würde: “Aha, bei hohen Rundensummen wird Banking wichtiger” oder “Wenn ich deutlich zurückliege, muss ich aggressiver werden”? Dann könnte sie auch in neuen Situationen vernünftige Entscheidungen treffen, ohne dass wir jeden einzelnen Fall vorbereitet haben.
Genau hier kommen neuronale Netze ins Spiel. Statt 75.000 Tabelleneintragen bauen wir eine lernende Funktion, die Muster erkennt und verallgemeinert. Das ist der Unterschied zwischen einem Spickzettel und echtem Verständnis.
Funktionsapproximation statt Lookup Tables
Die Grundidee ist elegant: Anstatt für jeden Zustand explizit zu speichern, was zu tun ist, trainieren wir ein neuronales Netz, das diese Zuordnung lernt.
# Alter Ansatz: Lookup Table
def lookup_table_approach(my_score, opp_score, round_sum):
table = {(10, 5, 8): "BANK", (10, 5, 9): "CONTINUE", ...} # 75.000+ Einträge!
return table.get((my_score, opp_score, round_sum), "CONTINUE")
# Neuer Ansatz: Neuronales Netz
def neural_network_approach(my_score, opp_score, round_sum):
features = [my_score/50, opp_score/50, round_sum/30] # Normalisierte Eingabe
return neural_network.predict(features) # Funktioniert für beliebige Eingaben!Ein neuronales Netz kann mit Situationen umgehen, die es nie explizit gesehen hat. Es interpoliert zwischen bekannten Zuständen und kann so auch bei eine vernünftige Entscheidung treffen, selbst wenn es diesen exakten Zustand nie im Training gesehen hat.
Das eröffnet völlig neue Möglichkeiten: Wir können gegen unbekannte Gegner spielen, Spielregeln anpassen oder sogar neue Strategien entdecken, die über unsere ursprünglichen Annahmen hinausgehen.
Neuronale Netze verstehen – Die wichtigsten Konzepte
Bevor wir unsere ersten neuronalen Netze für Push Your Luck entwickeln, müssen wir die Grundlagen verstehen. Keine Sorge – ich halte mich an das Wesentliche und erkläre alles am konkreten Beispiel.
Die Bausteine eines neuronalen Netzes
Ein neuronales Netz ist im Grunde eine sehr flexible Funktion, die lernen kann, Eingaben (wie Spielzustände) auf Ausgaben (wie Aktionen) abzubilden. Die wichtigsten Komponenten:
- Neuronen: Die Grundbausteine – jedes nimmt mehrere Eingaben, rechnet damit, und gibt ein Ergebnis weiter
- Layer (Schichten): Gruppen von Neuronen, die zusammenarbeiten
- Aktivierungsfunktion: Entscheidet, ob und wie stark ein Neuron “feuert” ( ist Standard)
- Gewichte: Die “Einstellungen” des Netzes, die beim Training angepasst werden
Für Push Your Luck könnte unsere Architektur so aussehen:
- Input Layer: 5 Features (mein Score, Gegner Score, Rundensumme, etc.)
- Hidden Layers: 128 → 64 → 32 Neuronen (Mustererkennung)
- Output Layer: 2 Werte (für jede mögliche Aktion)
Drei Wege, Spielwissen zu repräsentieren
Es gibt drei grundsätzlich verschiedene Ansätze, wie ein neuronales Netz Spielwissen codieren kann:
Value Function V(s): “Wie gut ist diese Situation?”
def value_function(game_state):
features = encode_state(game_state)
value = value_network.predict(features)[0] # Eine Zahl
return value # z.B. 0.73 = "73% Gewinnchance von hier aus"Die Value Function bewertet Zustände, aber wählt nicht direkt Aktionen. Wir müssten zusätzliche Logik entwickeln: “Wenn Banking zu Zustand mit Value 0.8 führt und Continuing zu 0.7, dann banke.”
Policy π(s): “Was soll ich tun?”
def policy_function(game_state):
features = encode_state(game_state)
probabilities = policy_network.predict(features)[0] # [prob_continue, prob_bank]
return probabilities # z.B. [0.3, 0.7] = "30% continue, 70% bank"Wichtig: Diese Wahrscheinlichkeiten sind Handlungswahrscheinlichkeiten, nicht Gewinnwahrscheinlichkeiten! [0.3, 0.7] bedeutet “wähle 30% der Zeit continue, 70% der Zeit bank” – nicht “continue hat 30% Gewinnchance”.
Q-Function Q(s,a): “Wie gut ist diese Aktion hier?”
def q_function(game_state):
features = encode_state(game_state)
q_values = q_network.predict(features)[0] # [Q(s,continue), Q(s,bank)]
return q_values # z.B. [0.65, 0.73] = "continue: 65%, bank: 73% Gewinnchance"Die Q-Function ist oft der beste Kompromiss: Sie bewertet jede Aktion direkt, und die Entscheidung ist einfach: “Wähle die Aktion mit dem höchsten Q-Wert.”
Lernmethoden: Woher kommt das Wissen?
Neuronale Netze sind nur so gut wie die Daten, von denen sie lernen. Es gibt drei Hauptansätze:
| Lernmethode | Datenquelle | Vorteile | Nachteile | Push Your Luck Beispiel |
|---|---|---|---|---|
| Supervised Learning | Labeled Beispiele von verschiedenen Quellen | Stabil, schnell, vorhersagbar | Begrenzt durch Trainingsdaten | Lerne von 10.000 Spielsituationen mit “korrekten” Aktionen |
| Imitation Learning | Experten-Demonstrationen (unser DP AI) | Kopiert bewährte Strategien, sehr stabil | Kann nie besser werden als der Experte | ”Mache immer das, was Dynamic Dan gemacht hätte” |
| Reinforcement Learning | Eigene Spielerfahrung (Trial & Error) | Kann neue Strategien entdecken, sehr flexibel | Instabil, langsam, unvorhersagbar | Spiele 1 Million Runden und lerne aus Siegen/Niederlagen |
Jeder Ansatz hat Vor- und Nachteile: Supervised Learning ist stabil aber begrenzt, Reinforcement Learning ist flexibel aber unberechenbar. Wir werden alle drei ausprobieren und sehen, was für Push Your Luck am besten funktioniert.
Supervised Learning: Den Experten kopieren
Die Idee: Warum das Rad neu erfinden?
Wir haben bereits die perfekte Push Your Luck Strategie: unsere Dynamic Programming AI. Sie trifft optimale Entscheidungen, aber braucht 75.000 Tabelleneintrage und stundenlange Vorberechnungen. Was wäre, wenn wir ein neuronales Netz trainieren könnten, das genauso spielt wie Dynamic Dan – aber 1000x schneller läuft?
Das ist die Grundidee des Imitation Learning: Wir lassen unseren Experten tausende von Entscheidungen treffen, zeichnen alles auf, und trainieren dann ein neuronales Netz, diese Entscheidungen zu imitieren. Wie ein Schachschüler, der die Züge eines Großmeisters studiert.
Datensammlung: Der Experte am Werk
Zuerst brauchen wir Trainingsdaten. Wir erstellen tausende von zufälligen Spielsituationen und fragen unsere DP AI: “Was würdest du hier tun?”
def collect_expert_data(dp_ai: MonteCarloDP_AI, n_samples: int = 15000) -> list:
training_data = []
for _ in range(n_samples):
# Zufällige aber realistische Spielsituationen
my_score = random.randint(0, 49)
opp_score = random.randint(0, 49)
round_sum = random.randint(1, 25)
game_state = GameState(
player_scores=(my_score, opp_score),
current_player=0,
current_round_sum=round_sum,
game_over=False,
winner=None
)
# Frage den Experten
expert_action = dp_ai.make_decision(game_state)
# Kodiere als Lernbeispiel
features = np.array([
my_score / 50.0, # Normalisiert auf 0-1
opp_score / 50.0,
round_sum / 30.0,
(my_score - opp_score + 50) / 100.0, # Punktedifferenz
min(1.0, round_sum / 15.0) # Risiko-Indikator
])
label = 1.0 if expert_action == PlayerAction.BANK_POINTS else 0.0
training_data.append((features, label))
return training_dataDiese Feature-Kodierung ist entscheidend: Wir müssen die Spielsituation in eine Form bringen, die das neuronale Netz verstehen kann. Alle Werte werden auf 0-1 normalisiert, damit das Training stabil läuft.
Training: Von Beispielen zur Strategie
Mit 15.000 Trainingsbeispielen können wir nun unser neuronales Netz trainieren. Wir verwenden einen Multi-Layer Perceptron (MLP) – ein klassisches neuronales Netz mit mehreren versteckten Schichten:
from sklearn.neural_network import MLPClassifier
# Netzwerk-Architektur: 5 → 64 → 32 → 1
model = MLPClassifier(
hidden_layer_sizes=(64, 32), # Zwei versteckte Schichten
activation='relu', # Standard-Aktivierungsfunktion
max_iter=200, # Maximum 200 Trainingsiterationen
random_state=42
)
# Training
model.fit(X_train, y_train)
# Test
test_acc = model.score(X_test, y_test)
print(f"Test accuracy: {test_acc:.3f}") # Typisch: 98%+Das Ergebnis ist beeindruckend: Unser Netz erreicht über 98% Genauigkeit auf dem Testdatensatz. Das bedeutet, es trifft in 98 von 100 Fällen dieselbe Entscheidung wie unser perfekter Experte.
Die Supervised Learning AI in Aktion
class SLPlayer:
def __init__(self, name: str, model_path: str):
self.name = name
self.model = joblib.load(model_path) # Lade trainiertes Modell
def make_decision(self, game_state: GameState) -> PlayerAction:
if game_state.current_round_sum == 0:
return PlayerAction.CONTINUE_ROLLING
# Kodiere Spielzustand
my_score = game_state.player_scores[game_state.current_player]
other_scores = [game_state.player_scores[i] for i in range(len(game_state.player_scores))
if i != game_state.current_player]
opp_score = max(other_scores) if other_scores else 0
features = np.array([[
my_score / 50.0,
opp_score / 50.0,
game_state.current_round_sum / 30.0,
(my_score - opp_score + 50) / 100.0,
min(1.0, game_state.current_round_sum / 15.0)
]])
# Schnelle Vorhersage
prob_bank = self.model.predict_proba(features)[0][1]
return PlayerAction.BANK_POINTS if prob_bank > 0.5 else PlayerAction.CONTINUE_ROLLINGDas Ergebnis: Fast perfekt, aber viel schneller
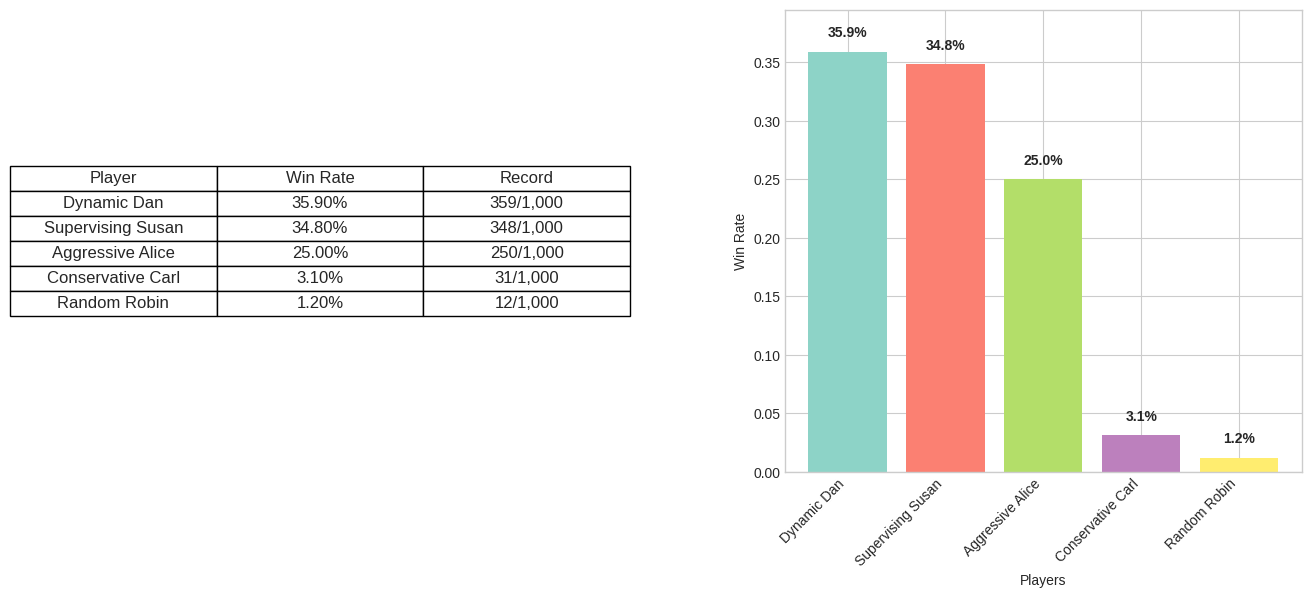
Im Turnier zeigt sich die Stärke des Supervised Learning: Unsere “Supervising Susan” spielt praktisch genauso gut wie Dynamic Dan, aber ist 1000x schneller. Keine Vorberechnungen, keine riesigen Lookup-Tabellen – einfach Feature eingeben, Entscheidung bekommen.
Das ist die Magie des Supervised Learning: Wir komprimieren das gesamte Wissen unseres Experten in ein kompaktes neuronales Netz, das überall eingesetzt werden kann. Selbst auf einem Smartphone könnte diese KI in Echtzeit optimale Push Your Luck Entscheidungen treffen.
Aber Supervised Learning hat auch seine Grenzen: Es kann nie besser werden als der ursprüngliche Experte. Was wäre, wenn es Strategien gibt, die selbst unser perfektes Dynamic Programming übersehen hat? Dafür brauchen wir einen anderen Ansatz: Reinforcement Learning.
Reinforcement Learning: Lernen durch Erfahrung
Supervised Learning kann nur so gut werden wie sein Lehrer. Aber was wäre, wenn eine KI völlig selbstständig Push Your Luck lernen könnte? Ohne Expertendemonstrations, ohne vorgegebene Strategien – nur durch millionenfaches Spielen und Lernen aus Erfolg und Misserfolg?
Das ist die Grundidee von Reinforcement Learning (RL): Eine KI spielt unzählige Partien, bekommt am Ende Feedback (“Du hast gewonnen!” oder “Du hast verloren!”), und lernt daraus, welche Entscheidungen zu Erfolg führen. Wie ein Kind, das Fahrradfahren lernt – durch Hinfallen, Aufstehen, und es nochmal versuchen.
Das Gym Environment: Push Your Luck als Trainingsumgebung
Für RL brauchen wir eine standardisierte Spielumgebung. Wir nutzen das OpenAI Gym Framework – den Industriestandard für RL-Experimente:
class PushYourLuckEnv(gym.Env):
def __init__(self, opponents=None):
self.opponents = opponents or [ConservativeAI("Bot", 18)]
# Aktionsraum: 0 = CONTINUE, 1 = BANK
self.action_space = spaces.Discrete(2)
# Zustandsraum: 5 normalisierte Features
self.observation_space = spaces.Box(low=0.0, high=1.0, shape=(5,), dtype=np.float32)
def step(self, action):
# Führe Aktion aus, berechne Reward, gib neuen Zustand zurück
...
return observation, reward, terminated, infoDas Herzstück ist die Reward-Funktion – sie definiert, was “gut” und “schlecht” ist:
- +1.0: Spiel gewonnen
- -1.0: Spiel verloren
- +0.05 × gewonnene_punkte: Kleine Belohnung für Fortschritt
- -0.1: Strafe für sinnloses Banking (0 Punkte)
Deep Q-Networks: Das Gehirn unserer RL-KI
Unser RL-Agent nutzt Deep Q-Learning (DQN) – eine der erfolgreichsten RL-Methoden. Die Idee: Trainiere ein neuronales Netz, das für jeden Zustand und jede Aktion den “Q-Wert” vorhersagt – die erwartete Belohnung, wenn man diese Aktion ausführt.
# DQN Architektur: 5 → 128 → 128 → 64 → 2
model = DQN(
'MlpPolicy', env,
learning_rate=1e-3,
batch_size=64,
# Exploration Schedule: 40% der Zeit explorieren
exploration_fraction=0.4,
exploration_initial_eps=1.0, # Start: 100% zufällig
exploration_final_eps=0.02, # Ende: 2% zufällig
policy_kwargs=dict(net_arch=[128, 128, 64])
)
model.learn(total_timesteps=100_000)Das Exploration-Exploitation Dilemma
Hier liegt eine der größten Herausforderungen von RL: Soll der Agent das tun, was er bereits als gut erkannt hat (Exploitation), oder neue Dinge ausprobieren (Exploration)?
Unser DQN startet mit 100% zufälligen Aktionen und reduziert das langsam auf 2%. Das ist, als würde ein Fahranfänger anfangs völlig wild lenken und erst nach tausenden Fahrstunden eine konsistente Fahrweise entwickeln.
Warum RL bei Push Your Luck enttäuscht
Im direkten Vergleich schneidet unser RL-Agent deutlich schlechter ab als Dynamic Programming oder Supervised Learning. Warum?
1. Sparse Rewards RL bekommt nur am Spielende Feedback (“Gewonnen” oder “Verloren”). Das ist, als würde man jemandem Schach beibringen, aber nur nach 50 Zügen sagen “Du hast verloren” – ohne zu erklären, welche der 50 Entscheidungen schlecht waren.
2. Trainingsinstabilität RL ist berüchtigt dafür, instabil zu sein. Manchmal lernt der Agent eine gute Strategie, vergisst sie aber wieder durch späteres Training. Das nennt sich “Catastrophic Forgetting”.
3. Hyperparameter-Sensitivität RL ist extrem empfindlich gegenüber Einstellungen. Ein falscher Learning Rate, und das Training kollabiert. Eine schlecht gewählte Exploration-Rate, und der Agent entdeckt nie gute Strategien.
4. Sample Inefficiency Während Supervised Learning aus 15.000 Expertentscheidungen lernen kann, braucht RL Millionen von Spielerfahrungen. Das ist wie der Unterschied zwischen einem Lehrbuch und reiner Trial-and-Error-Methode.
Obwohl RL bei Push Your Luck nicht überzeugt, gibt es Bereiche, wo es unschlagbar ist: Bei Go und Schach gibt es keine “perfekten” Experten – RL-Systeme haben die besten menschlichen Spieler übertroffen und völlig neue Strategien entdeckt. Wenn wir nicht sicher wissen, was “optimal” ist, kann RL durch pure Exploration neue Lösungen finden.
Verbesserungsansätze: Wie RL besser werden könnte
| Ansatz | Grundidee | Vorteil für Push Your Luck | Analogie |
|---|---|---|---|
| Curriculum Learning | Graduelle Schwierigkeitssteigerung: Erst gegen Random AIs, dann Conservative, dann Aggressive | Stabiles Lernen ohne Überforderung | Matheunterricht: Addition → Multiplikation → Integration |
| Self-Play | Agent spielt gegen frühere Versionen seiner selbst | Kontinuierlich stärkere Gegner, kein Overfitting | Schachtraining gegen eigene alte Partien |
| Enhanced Reward Shaping | Zusätzliches Feedback: “Gut bei 15 gebankt”, “Zu riskant bei 25” | Schnelleres Lernen durch direktes Feedback | Fahrstunden mit Kommentaren statt nur “Bestanden/Durchgefallen” |
| Opponent Modeling | Lerne Gegnerstile und passe Strategie an | Dynamische Anpassung: aggressiv vs. Conservative AI | Poker: Tight gegen Loose Players, Loose gegen Tight Players |
| Population-Based Training | Viele Agents trainieren gleichzeitig, beste überleben | Diversität der Strategien, natürliche Selektion | Evolutionsbiologie: Überleben der Angepasstesten |
Zwischen Fazit: RL als Forschungsgrenzland
Reinforcement Learning ist faszinierend und mächtig, aber auch schwierig und unberechenbar. Für Push Your Luck, wo wir bereits optimale Lösungen haben, ist es überdimensioniert. Aber für wirklich unbekannte Probleme, wo keine Experten existieren und neue Strategien entdeckt werden müssen, ist RL unersetzlich.
In unserem Fall bleibt Dynamic Programming mit Supervised Learning die beste Lösung.
Hyperparameter-Optimierung: Die Kunst des Feintunings
Auch wenn RL in unserem Fall nicht die passende Lösung ist, möchte ich noch auf eine wichtige Herausforderung eingehen. Bei meinen Experimenten mit RL war es unglaublich aufwendig, die Hyperparameter zu optimieren.
Hyperparameter sind die “Einstellungen” eines maschinellen Lernsystems – die Werte, die wir vor dem Training festlegen müssen:
- Learning Rate: Wie schnell lernt das Netz? (0.001, 0.0001, …)
- Batch Size: Wie viele Erfahrungen gleichzeitig? (64, 128, 256)
- Exploration Rate: Wie lange zufällig handeln? (30%, 50% der Zeit)
- Network Architecture: Wie groß das Netz? (128→64 oder 256→128→64)
Das Problem: 10 Learning Rates × 4 Batch Sizes × 5 Exploration Rates × 3 Architekturen = 600 Kombinationen. Jede braucht 2-3 Stunden Training. Das sind 75 Tage kontinuierliches Training.
Trial-and-Error: Der Weg ins Chaos
Mein erster Ansatz war klassisches “Trial-and-Error”: Parameter testen, schlecht → andere versuchen, besser → nächsten Parameter ändern… Nach 20 getesteten Kombinationen war ich mehr verwirrt als erleuchtet. Eine bessere Methode musste her.
Bayesian Optimization: Intelligente Parametersuche
Die Lösung heißt Optuna – ein Framework für automatische Hyperparameter-Optimierung. Das System lernt aus jedem Experiment und wird bei der Auswahl der nächsten Parameter immer intelligenter.
def optimize_dqn_hyperparameters(trial):
# Optuna schlägt Parameter vor
params = {
'learning_rate': trial.suggest_float('learning_rate', 1e-5, 1e-2, log=True),
'batch_size': trial.suggest_categorical('batch_size', [64, 128, 256]),
'exploration_fraction': trial.suggest_float('exploration_fraction', 0.1, 0.6)
}
# Trainiere und bewerte Modell
model = DQN('MlpPolicy', env, **params)
model.learn(total_timesteps=200_000)
win_rate = evaluate_in_tournament(model)
return win_rate
# Starte intelligente Suche
study = optuna.create_study(direction='maximize')
study.optimize(optimize_dqn_hyperparameters, n_trials=50)Über RL hinaus: Universelle Anwendbarkeit
Optuna funktioniert nicht nur für neuronale Netze. Wir könnten es genauso für unsere Aggressive AI einsetzen:
def optimize_aggressive_ai(trial):
base_threshold = trial.suggest_int('base_threshold', 10, 25)
behind_bonus = trial.suggest_int('behind_bonus', 0, 10)
ai = EnhancedAggressiveAI(base_threshold=base_threshold, behind_bonus=behind_bonus)
win_rate = run_tournament([ai, conservative_ai, random_ai], 1000)
return win_rateSo könnten wir herausfinden, ob ein Schwellenwert von zum Beispiel 23 mit Behind-Bonus 7 besser funktioniert als unsere manuell gewählten Werte.
Effizienz durch Intelligenz
Nach 50 Optuna-Experimenten statt 600 manuellen Tests hatte ich die besten Hyperparameter gefunden. Optuna reduzierte die Suchzeit von 75 Tagen auf 2 Tage – und fand dabei bessere Parameter, als ich sie manual je entdeckt hätte.
Das zeigt ein wichtiges Prinzip der modernen KI-Entwicklung: Automatisierung der Automatisierung. Wir nutzen intelligente Algorithmen, um andere Algorithmen zu optimieren. Dieselben Prinzipien funktionieren überall – ob bei neuronalen Netzen, traditionellen Algorithmen oder sogar bei der Optimierung von Geschäftsprozessen.
Theoretische Einordnung: Was haben wir eigentlich gebaut?
Klassifikation unserer KI-Ansätze
Nach dieser langen Reise durch verschiedene KI-Techniken ist es Zeit für einen Schritt zurück. Wir haben sieben völlig unterschiedliche Ansätze entwickelt – aber wie lassen sie sich fachlich einordnen?
Model-Based vs. Model-Free: Wer kennt die Spielregeln?
Model-Based (kennt Spielregeln):
Der erste wichtige Unterschied: Welche unserer KIs verstehen explizit, wie Push Your Luck funktioniert? Model-Based Ansätze nutzen mathematisches Wissen über Wahrscheinlichkeiten und Spielregeln für ihre Entscheidungen.
| Ansatz | Spielverständnis | Analogie |
|---|---|---|
| ProbabilisticAI | Nutzt P(bust) = 1/6 analytisch | Mathematiker mit Formelsammlung |
| Dynamic Programming | Vollständiges Spielmodell + Gegnerverhalten | Strategiebuch mit allen Situationen |
| Rule-based AIs | Domänenspezifische Heuristiken | Erfahrener Spieler mit Faustregeln |
Model-Free (lernt aus Erfahrung):
Model-Free Ansätze hingegen lernen ausschließlich aus Beobachtungen und Erfahrungen, ohne die zugrundeliegenden Spielmechaniken zu verstehen.
| Ansatz | Spielverständnis | Analogie |
|---|---|---|
| Supervised Learning | Lernt nur von Expertenbeispielen | Imitiert Meister ohne Regelverständnis |
| Reinforcement Learning | Trial-and-Error Entdeckung | Lernt durch millionenfaches Ausprobieren |
| Random AI | Kein Spielverständnis | Würfelt alle Entscheidungen |
Lernparadigmen: Woher kommt das Wissen?
Eine andere wichtige Klassifikation: Woher stammt eigentlich das Wissen unserer KIs? Manche nutzen (menschliches) Expertenwissen, andere entdecken Strategien völlig selbstständig.
| Wissensquelle | Ansätze | Vorteil | Nachteil |
|---|---|---|---|
| Expertenwissen | Supervised Learning, Rule-based AIs | Schnell, zuverlässig | Begrenzt durch Expertenqualität |
| Selbstentdeckung | Dynamic Programming, Reinforcement Learning | Kann Experten übertreffen | Langsam, unvorhersagbar |
| Hybridansätze | Enhanced RL (mit Reward Shaping) | Kombination aus beidem | Komplex zu designen |
Temporal vs. Non-Temporal Learning
Ein weiterer wichtiger Unterschied liegt darin, wie unsere KIs mit der zeitlichen Abfolge von Entscheidungen umgehen.
| Lerntyp | Ansätze | Charakteristik | Vorteil |
|---|---|---|---|
| Temporal Difference | DQN, Enhanced RL | Lernt aus Entscheidungssequenzen, versteht langfristige Konsequenzen | Berücksichtigt zukünftige Auswirkungen |
| Non-Temporal | Supervised Learning, Rule-based AIs | Behandelt Entscheidungen isoliert, vergisst nie Gelerntes | Stabil und vorhersagbar |
Fundamentale Trade-offs
Jeder unserer KI-Ansätze macht bewusste Kompromisse – es gibt keine Lösung, die in allen Bereichen optimal ist. Diese Trade-offs zu verstehen ist entscheidend für die Wahl der richtigen Methode.
Der erste wichtige Kompromiss betrifft Optimalität vs. Flexibilität: Unser Dynamic Programming AI ist mathematisch perfekt für Push Your Luck – aber nur für Push Your Luck. Ändern wir eine einzige Regel (z.B. “Bust bei 1 und 2”), müssen wir alles neu berechnen. Reinforcement Learning hingegen spielt suboptimal, kann aber binnen Stunden neue Spielvarianten lernen.
Eng verwandt damit ist der Trade-off zwischen Trainingszeit und Laufzeit: Dynamic Programming braucht stundenlange Vorberechnungen und GB an Speicher, trifft dann aber sofort perfekte Entscheidungen. Supervised Learning trainiert in Minuten und läuft auf jedem Smartphone.
Ein weiterer Aspekt ist der Konflikt zwischen Verständlichkeit und Performance: Conservative AI mit “Bank bei 8 Punkten” kann jeder verstehen und nachvollziehen. Neuronale Netze mit 10.000 Parametern sind Black Boxes – wir wissen nicht, warum sie bestimmte Entscheidungen treffen. Dieser Trade-off wird in Bereichen wie Medizin oder Justiz - wo Erklärbarkeit entscheidend ist - immer wichtiger.
Schließlich gibt es noch den Gegensatz zwischen Stabilität und Entdeckungspotenzial: Supervised Learning ist wie ein Muster Schüler: Es lernt zuverlässig das, was man ihm beibringt – aber nie mehr. Reinforcement Learning ist wie ein kreativ-chaotischer Erfinder: Es kann revolutionäre Durchbrüche machen (siehe AlphaGo’s völlig neue Züge), aber auch spektakulär scheitern. Diese Unberechenbarkeit macht RL für Forschung wertvoll, für Produktivsysteme aber auch riskant.
Diese Trade-offs erklären, warum es nicht die “eine beste KI-Methode” gibt. Die optimale Wahl hängt immer vom konkreten Problem ab: Brauche ich Perfektion oder Geschwindigkeit? Interpretierbarkeit oder Performance? Sicherheit oder Innovation?
Fazit
Was als einfaches Würfelspiel begann, wurde zur Reise durch die Landschaft der KI-Entwicklung. Von mathematischer Optimierung über Dynamic Programming bis zu Deep Learning – Push Your Luck hat sich als perfektes Experimentierfeld erwiesen, um die Stärken und Schwächen verschiedener Ansätze zu verstehen.
Es gibt keine universell beste KI-Technik - jeder Ansatz macht bewusste Kompromisse zwischen Optimalität und Flexibilität, zwischen Verständlichkeit und Performance, zwischen Stabilität und Innovation. Die Kunst liegt darin, für jedes Problem die richtige Wahl zu treffen.
Besonders faszinierend war die Erkenntnis, dass vermeindlich vollständige Optimierung verheerend sein kann. Unsere “Smart Sam” mit ihrer Expected-Value-Strategie war mathematisch korrekt – aber für das falsche Problem. Sie optimierte Punkte statt Gewinnwahrscheinlichkeit und ignorierte völlig den Spielkontext. Eine simple Aggressive AI, die wenigstens verstand, dass Push Your Luck ein Rennen ist, schlug sie mühelos. Korrekte Problem Identifikation schlägt elegante Lösung – eine Lektion, die weit über Würfelspiele hinausreicht.
Die Zukunft vorherwürfeln
Push Your Luck mag simpel erscheinen, aber die Prinzipien, die wir hier erkundet haben, finden sich in allen Bereichen der künstlichen Intelligenz wieder: Autonomes Fahren muss zwischen Sicherheit und Effizienz abwägen, Empfehlungssysteme zwischen Exploration neuer Inhalte und Exploitation bewährter Präferenzen, Börsen-Algorithmen zwischen konservativen und riskanten Strategien.
Die Reise zeigt auch, wohin sich die KI-Entwicklung bewegt: Weg von monolithischen “Super-Algorithmen” hin zu intelligenten Kombinationen verschiedener Techniken. Unsere beste Lösung war letztendlich ein Hybrid aus mathematischer Optimierung (Dynamic Programming) und schneller Funktionsapproximation (Supervised Learning).
Der Code zum Experimentieren
Alle Implementierungen, Experimente und trainierten Modelle sind verfügbar im GitHub Repository. Das Repository enthält den vollständigen Code als interaktives Jupyter Notebook zum Nachexperimentieren und Weiterentwickeln - und auch ein paar fertig trainierte Modelle.
So viel sei noch gesagt: Die Reise in die Welt der künstlichen Intelligenz auf diesem Blog hat gerade erst begonnen. Push Your Luck war nur der Anfang …
Meme Quelle: Dave’s Garage